Доверительный интервал применяют в статистике по следующим ключевым причинам:
Содержание
Основное назначение доверительного интервала
- Оценка точности статистических показателей
- Учет случайной изменчивости данных
- Определение диапазона вероятных значений параметра
- Сравнение групп в исследованиях
- Принятие решений на основе статистических данных
Преимущества перед точечной оценкой
| Характеристика | Доверительный интервал | Точечная оценка |
| Информативность | Показывает диапазон возможных значений | Дает единственное значение |
| Надежность | Учитывает случайную ошибку | Игнорирует вариабельность |
| Интерпретация | Позволяет оценить точность | Не показывает неопределенность |
Как работает доверительный интервал
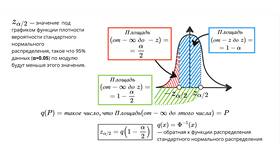
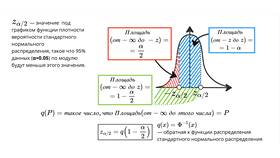
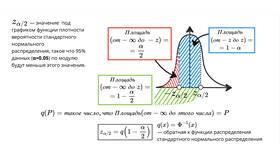
Принципы построения доверительного интервала:
- Выбор уровня доверия (обычно 95%)
- Расчет стандартной ошибки измерения
- Определение критического значения распределения
- Вычисление границ интервала
- Интерпретация полученного диапазона
Факторы, влияющие на ширину интервала:
- Объем выборки (чем больше, тем уже интервал)
- Изменчивость данных (чем больше, тем шире интервал)
- Уровень доверия (чем выше, тем шире интервал)
Применение в различных областях
| Область | Пример использования |
| Медицина | Оценка эффективности лечения |
| Экономика | Прогнозирование экономических показателей |
| Социология | Анализ результатов опросов |
| Технические науки | Контроль качества продукции |
Ошибки в интерпретации
Распространенные заблуждения:
- Считать, что параметр точно находится в интервале
- Путать доверительный интервал с диапазоном данных
- Игнорировать уровень доверия при сравнении
- Использовать неадекватные методы построения
- Не учитывать распределение данных
Правильная интерпретация:
- 95% доверительный интервал означает, что в 95% случаев метод дает интервал, содержащий истинный параметр
- Ширина интервала отражает точность оценки
- Пересекающиеся интервалы не всегда означают отсутствие различий
- Выбор уровня доверия зависит от задачи
Заключение
Доверительный интервал является мощным инструментом статистического анализа, позволяющим оценить не только величину параметра, но и точность его измерения. Правильное использование доверительных интервалов помогает принимать более обоснованные решения в условиях неопределенности и избегать ошибочных выводов из статистических данных.